Après avoir vu le point, si nous passions à la ligne ? Ou plus exactement, au segment de droite.
Sur une feuille de papier, tracer un segment de droite entre deux points est une chose simple : un crayon, un règle, on positionne la règle sur les deux points et l'on trace un trait en tenant fermement cette dernière.
Le trait a alors une allure continue ; du moment que l'on n'utilise pas un microscope pour en détailler la composition. Et c'est une représentation suffisante, dans la plupart des cas, de l'objet mathématique sous-jacent.
Sur un écran d'ordinateur, c'est un tout autre problème. En effet, un écran traditionnel est constitué d'une matrice de petits carreaux, les pixels. Les pixels des écrans récents sont très petits et malgré cela, tracer un beau segment de droite n'est pas si simple. Alors imaginez avec les gros carreaux formant les affichages d'anciens ordinateurs ?
Plutôt que de l'imaginer, vous pouvez même faire une expérience.
Prenez une feuille à petits carreaux, choisissez un point de départ que vous coloriez en noir, un point d'arrivée que vous coloriez en noir. L'exercice consiste alors à colorier les carreaux intermédiaires afin de tracer un segment de droite.
Si la réalisation est très simple pour des segments de droite horizontaux, vertiaux ou diagonaux, les droites plus quelconques, elles, demandent un peu plus d'attention afin d'obtenir un beau tracé, équilibré.
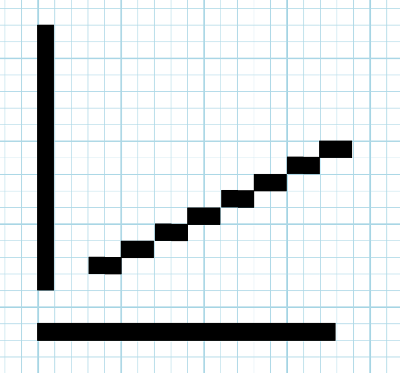
Une stratégie peut être de prendre une règle, de tracer un trait fin entre les milieux des deux cases d'extrémités et de colorier ensuite les cases traversées par le trait.
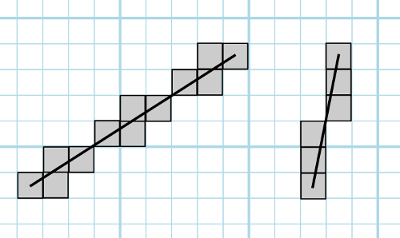
Il y a de l'idée, mais la droite, avec certaines orientations, est épaisse par endroit. Avec des gros pixels, cela ne va pas bien rendre.
Une autre idée est d'utiliser la forme mathématique d'une droite : $y = ax + b$. En
ajustant correctement a et b et faisant varier x sur les coordonnées de l'écran, on
devrait trouver y.
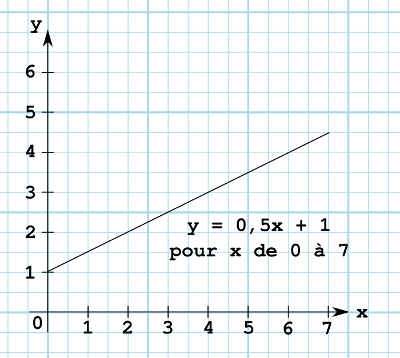
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| y | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 |
La solution fonctionne bien... jusqu'à ce que a soit supérieur à 1. Au-delà de 1, le tracé
du segment à l'écran n'est plus continu, mais comporte des trous !
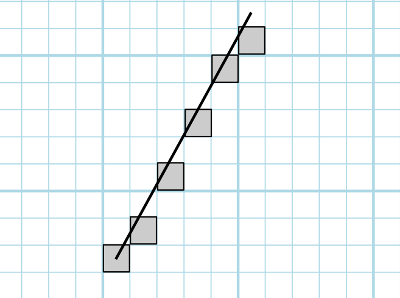
Et c'est sans parler du cas où l'on voudrait tracer un segment vertical. En effet, avec
l'idée de faire varier les x, pour un segment vertical, x ne prend qu'une valeur. Et donc
y une seule valeure aussi. Ce qui donne... un beau point. C'est normal puisqu'à une valeur de x
on associe une et une seule valeur de y.
Cette manière de tracer des segments de droite semble ne pas fonctionner, et pourtant, c'est première idée n'est pas si mauvaise. Elle nécessite juste un petit ajustement.
Puisque la méthode de balayage des x fonctionne sur les segments de droites allant d'une
pente nulle, l'horizontale, à une pente de 1, la diagonale, peut-être faut-il changer un
peu d'angle pour les segments de droite allant de la diagonale à la verticale ?
Pour cette partie-là, est-ce qu'il ne suffirait pas de poser : $x = a'y + b'$ ? C'est-à-dire
balayer les y pour obtenir les x, avec des coefficients ajustés en conséquence.
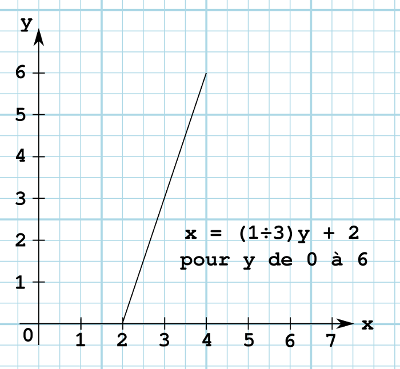
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| y | 2 | 2 + 1/3 | 2 + 2/3 | 3 | 3 + 1/3 | 3 + 2/3 | 4 |
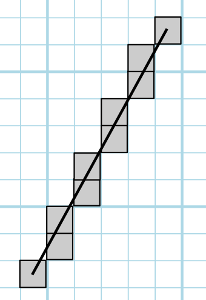
Ça fonctionne plutôt bien.
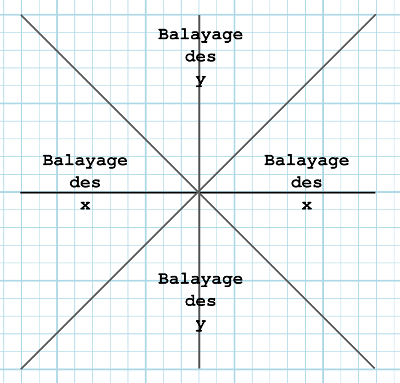
Par un jeu de symétries, le problème peut être résolu en séparant l'espace autour du point
de départ en huit espaces qui induiront l'utilisation d'un balayage des x ou des y. Ces
secteurs étant au nombre de huit, on les appelle des octants.
Pour simplifier le problème, on peut limiter les cas à deux d'entres eux en prenant pour
extrémité de départ le point le plus à gauche sur l'axe des x, par exemple. Il reste alors à considérer
dans lequel des quatre octants à la droite de ce point le segment va être tracé, et
choisir entre le balayage des x ou le balayage des y.
Pour décider de la méthode à appliquer, on peut commencer par calculer la pente de la droite.
Si les deux points sont (x, y) et (x', y'), alors la pente de la droite est $\frac{(y' - y)}{(x' - x)}$, le a
dans $y = ax + b$.
Cependant, en cas de droite verticale, on se retrouve avec une division par 0 (x' étant égal à x).
Si la droite est presque verticale, on peut aussi se retrouver avec des valeurs assez grandes et des
problèmes de capacités de calcul de la machine.
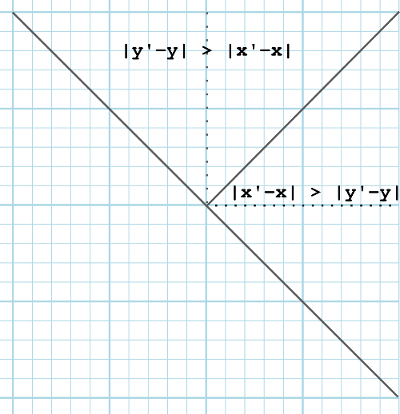
En fait, il n'est pas nécessaire de calculer la pente, car ce que l'on cherche à savoir où se situe la droite portant le segment par rapport à une horizontale, une verticale et une diagonale.
Et pour cela, il suffit d'une part de comparer les valeurs absolues de $(y' - y)$ et de $(x' -
x)$. Si dans le cas d'un balayage des y, on part du point le plus bas (tout comme on part du point
le plus à gauche pour le balayage des x), alors les secteurs sont utilisés de cette manière :
Un premier algorithme
J'obtiens donc une première idée d'algorithme qui ressemble grossièrement à ça :
- En entrée, on a deux points de coordonnées (x, y) et (x', y')
- Si x' est plus petit que x, échanger les valeurs de
xetx'ainsi que deyety' - Choix de l'octant en fonction de |y' - y| et de |x' - x|
- Si on fait un balayage des x, alors
- Calculer la pente $a = \frac{(y' - y)}{(x' - x)}$
- Calculer $b = \frac{x'y - xy'}{x'-x}$
- Pour tous les
x''dexàx', calculer $y'' = ax'' + b$. - Tracer un pixel en
(x'', y'').
- Si on fait un balayage des y, alors
- Si y' est plus petit que y, échanger les valeurs de
xetx'ainsi que deyety' - Calculer la pente $a = \frac{(x' - x)}{(y' - y)}$
- Calculer $b = \frac{y'x - yx'}{y'-y}$
- Pour tous les
y''deyày', calculer $x'' = ay'' + b$ - Tracer un pixel en
(x'', y'')
- Si y' est plus petit que y, échanger les valeurs de
Voici un algorithme de tracé de segment de droite qui fonctionne. Mais qui est aussi extrêmement lent. Dans un prochain article, nous verrons comment rendre ça sur le VG5000 en BASIC.