Triceraprog
La programmation depuis le Crétacé

Après avoir tracé des segments de droite à l'écran grâce au BASIC du VG5000µ, passons au cercle.

Si vous avez fait un peu de trigonométrie à l'école, vous devez savoir que, pour un angle α allant de 0 à 2π, tracer des points aux coordonnées (cos(α), sin(α)). Ces coordonnées sont multipliées par le rayon et déplacées au centre du cercle. Et c'est comme cela qu'il peut sembler de prime abord intéressant de tracer un cercle.

Cela ressemble à quelque chose comme ça.

• initialiser cx et cy avec les coordonnées du centre du cercle, r avec son rayon
• initialiser a à 0
• tant que $a < 2\pi$
  • $x = cx + r.cos(a)$
  • $y = cy + r.sin(a)$
  • tracer un point en (x, y)
  • augmenter a
• fin

Super simple.

Mais trop simple.

Dans l'algorithme ci-dessus, la ligne qui indique augmenter a n'indique pas de combien il faudrait augmenter a.

Lorsque l'on trace un cercle avec un crayon sur une feuille, on prend quelques points de références bien choisi, puis on interpole entre ces points pour tracer la courbe. Si on utilise un compas, c'est encore plus simple, il suffit de deux points de référence : le centre et un point du rayon.

Nous avons ici le même problème que lorsque l'on cherchait à tracer un segment de droite : l'espace de tracé des points à l'écran n'est pas continu. Il s'agit dans notre cas d'allumer des pixels de manière à provoquer l'illusion de la continuité.

S'ils sont trop tassés, c'est moche. S'ils sont trop espacés, ça fait des trous.

Prenons un exemple avec cx = 6, cy = 5 et r = 5. Augmentons a d'un dixième de π à chaque fois. Voilà ce que cela donne :

a	0.pi/10	1.pi/10	2.pi/10	3.pi/10	4.pi/10	5.pi/10	6.pi/10	7.pi/10	8.pi/10	9.pi/10
x	11	11	10	9	8	6	4	3	2	1
y	5	7	8	9	10	10	10	9	8	7

a	10.pi/10	11.pi/10	12.pi/10	13.pi/10	14.pi/10	15.pi/10	16.pi/10	17.pi/10	18.pi/10	19.pi/10
x	1	1	2	3	4	6	8	9	10	11
y	5	3	2	1	0	0	0	1	2	3

Traçons cela sur une grille.

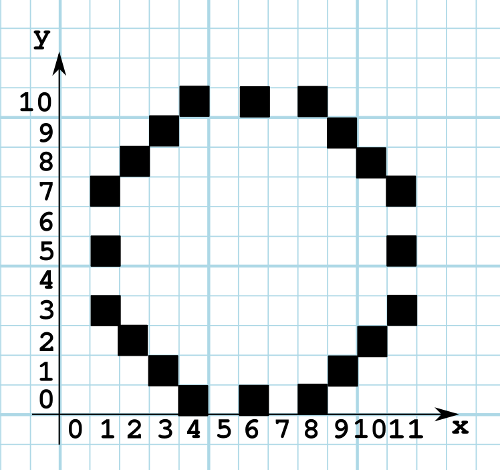
Tout comme avec le segment de droite au début, il y a des trous. Et si le rayon augmente, il y aura encore plus de trous. On peut se dire alors qu'on augmente a par de plus petites valeurs. Mais on voit sur le dessin qu'à certains endroits, les pixels sont adjacents. Cela signifierait qu'il faudrait, suivant les endroits, augmenter a différemment.

Arrêtons-nous là pour deux raisons : la première est que l'on sent bien que cela va nous amener vers des choses vraiment complexes. La seconde est que calculer le cosinus et le sinus sur une machine ancienne de ce type, c'est lent, très lent. Certes, notre affichage de pixel est lent lui aussi, n'ajoutons pas du lent au lent.

Mais alors que faire ?

Changer de stratégie, et surtout, d'équation de départ. L'équation d'un cercle est aussi celle-ci : $x^2 + y^2 - r^2 = 0$. Où r est le rayon. Un tel cercle est centré sur les coordonnées (0, 0) mais il suffit d'y ajouter les coordonnées du centre du cercle voulu pour le déplacer dans l'espace.

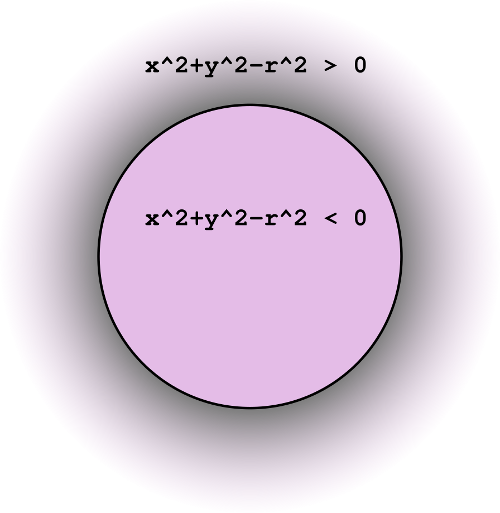
La deuxième chose que l'on va faire est, comme avant pour le segment de droite, de simplifier le problème en utilisant des octants, c'est-à-dire une division en huit secteurs. Ces secteurs sont choisis pour leurs axes de symétries sur le cercle de manière à ce que, pour un octant donnée, nous puissions nous occuper d'un cas très simple.

Je vous invite à aller voir l'image plus bas pour repérer les axes de symétries utilisés.

Une méthode

En commençant par le point le plus haut du cercle et sur l'octant en haut à droite, on peut réduire le problème à une courbe qui part dans la direction générale entre la droite et la diagonale droite-bas. Dans ce secteur, un pixel aura pour voisin suivant soit le pixel juste à sa droite, soit le pixel juste au-dessous celui à sa droite.

Si on trouve comment tracer ce petit morceau de courbe, il suffit de tracer les huit courbes symétriques sur le cercle pour obtenir la forme complète.

Comment choisir si le pixel suivant le pixel courant doit être celui à sa droite ou celui en diagonal ? En utilisant la partie gauche de la formule ci-dessus pour évaluer la position du cercle parfait par raport à un point situé entre les deux points éligibles.

Si le résultat est inférieur à 0, alors c'est que le point médian est à l'intérieur du cercle. On choisi alors le pixel à droite comme coordonnée suivante.

Si le résultat est supérieur à 0, alors c'est que le point médian est à l'extérieur du cercle. On choisi alors le pixel en bas à droite comme coordonnée suivante.

Et ainsi de suite jusqu'à ce que la coordonnée x soit supérieure à la coordonnée y, ce qui signal la fin de l'octant, puisque nous aurons alors atteint la diagonale.

Reprenons :

• initialiser cx et cy avec les coordonnées du centre du cercle, r avec son rayon
• initialiser (x, y) à (0, r), c'est à dire le point au sommet du cercle.
• tant que x ≤ y
  • tracer le pixel(x + cx, y + cy) et ses sept symétries.
  • calculer $m = (x+1)^2 + (y-0.5)^2 - r^2$
  • si m >= 0 alors $x \leftarrow x + 1$ et $y \leftarrow y - 1$
  • sinon $x \leftarrow x + 1$
• fin

Voyons ce que cela donne avec les même entrées que précédemment :

x	6	7	8	9
y	10	10	10	9
m	-3.75 (suivant à droite)	-0.75 (suivant à droite)	4.25 (suivant en bas à droite)	3.25

Le cercle n'a plus de trous, les pixels sont voisins et forment une illusion de continuité. Ce qui donne sur du papier quadrillé, avec en noir les coordonnées ci-dessus et en gris les différents symétriques.

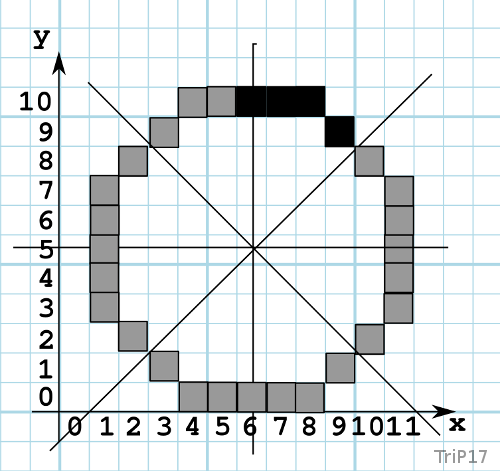
Note : cet algorithme n'est pas le seul possible et nous verrons lors de son implémentation qu'il peut être simplifié au niveau de ses calculs. Mais ceci est une autre histoire.

Note 2 : le second algorithme présenté est l'algorithme de tracé de cercle de Bresenham, du nom de son auteur.